En este tutorial rápido de GNU a los modelos estadísticos y gráficos, proporcionaremos un ejemplo de regresión lineal simple y aprenderemos cómo realizar un análisis estadístico básico de datos. Este análisis irá acompañado de ejemplos gráficos, lo que nos llevará más cerca de la producción de tramas y gráficos con Gnu R. Si no está familiarizado con el uso de R en absoluto, eche un vistazo al tutorial de requisitos previos: un tutorial rápido de Gnu R a las operaciones, funciones y estructuras de datos básicas.

Modelos y fórmulas en R

Entendemos un modelo en estadísticas como una descripción concisa de los datos. Dicha presentación de datos generalmente se exhibe con un fórmula matemática. R tiene su propia forma de representar relaciones entre variables. Por ejemplo, la siguiente relación y = c₀+C₁X₁+C₂X₂+… +C_norteX_norte+r está en r escrito como

y ~ x1+x2+...+xn,

que es un objeto de fórmula.

Ejemplo de regresión lineal

Proporcionemos ahora un ejemplo de regresión lineal para Gnu R, que consta de dos partes. En la primera parte de este ejemplo, estudiaremos una relación entre los rendimientos del índice financiero denominado en el dólar estadounidense y tales rendimientos denominados en el dólar canadiense. Además, en la segunda parte del ejemplo, agregamos una variable más a nuestro análisis, que son los retornos del índice denominado en euro.

Regresión lineal simple

Descargue el archivo de datos de ejemplo a su directorio de trabajo: regresión-exame-gnu-r.CSV

Ahora ejecutemos R en Linux desde la ubicación del directorio de trabajo simplemente por

$ R

y lea los datos de nuestro archivo de datos de ejemplo:

> Devoluciones<-read.csv("regression-example-gnu-r.csv",header=TRUE)

Puedes ver los nombres de las variables escribiendo

> Nombres (devoluciones)
[1] "USA" "Canadá" "Alemania"

Es hora de definir nuestro modelo estadístico y ejecutar regresión lineal. Esto se puede hacer en las siguientes líneas de código:

> y<-returns[,1]
> x1<-returns[,2]
> Devoluciones.lm<-lm(formula=y~x1)

Para mostrar el resumen del análisis de regresión, ejecutamos el resumen() función en el objeto devuelto devoluciones.lm. Eso es,

> Resumen (devoluciones.LM)
Llamar:
lm (fórmula = y ~ x1)
Derechos residuales de autor:
Min 1q mediana 3q max
-0.038044 -0.001622 0.000001 0.001631 0.050251
Coeficientes:
Estimarse ETS. Error t valor pr (> | t |)
(Intercepción) 3.174E-05 3.862e-05 0.822 0.411
X1 9.275E-01 4.880E-03 190.062 <2e-16 ***
---
Significado. Códigos: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.'0.1 "1
Error estándar residual: 0.003921 en 10332 grados de libertad
Múltiples R-cuadrado: 0.7776, R-cuadrado ajustado: 0.7776
Estadística F: 3.612e+04 en 1 y 10332 df, valor p: < 2.2e-16

Esta función genera el resultado correspondiente anterior. Los coeficientes estimados están aquí C₀~ 3.174E-05 y C₁ ~ 9.275E-01. Los valores p anteriores sugieren que la intersección estimada C₀ no es significativamente diferente de cero, por lo tanto, se puede descuidar. El segundo coeficiente es significativamente diferente de cero desde el valor p<2e-16. Therefore, our estimated model is represented by: y=0.93 x₁. Además, R-Squared es 0.78, lo que significa que aproximadamente el 78% de la varianza en la variable Y se explica por el modelo.

Regresión lineal múltiple

Agreguemos ahora una variable más a nuestro modelo y realizamos un análisis de regresión múltiple. La pregunta ahora es si agregar una variable más a nuestro modelo produce un modelo más confiable.

> x2<-returns[,3]
> Devoluciones.lm<-lm(formula=y~x1+x2)
> Resumen (devoluciones.LM)
Llamar:
lm (fórmula = y ~ x1 + x2)
Derechos residuales de autor:
Min 1q mediana 3q max
-0.0244426 -0.0016599 0.0000053 0.0016889 0.0259443
Coeficientes:
Estimarse ETS. Error t valor pr (> | t |)
(Intercepción) 2.385E-05 3.035E-05 0.786 0.432
X1 6.736E-01 4.978E-03 135.307 <2e-16 ***
x2 3.026E-01 3.783E-03 80.001 <2e-16 ***
---
Significado. Códigos: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.'0.1 "1
Error estándar residual: 0.003081 en 10331 grados de libertad
Múltiples R-cuadrado: 0.8627, R-cuadrado ajustado: 0.8626
Estadística F: 3.245E+04 en 2 y 10331 df, valor p: < 2.2e-16

Arriba, podemos ver el resultado del análisis de regresión múltiple después de agregar la variable x₂. Esta variable representa los rendimientos del índice financiero en euro. Ahora obtenemos un modelo más confiable, ya que el R-cuadrado ajustado es 0.86, que es mayor que el valor obtenido antes de igual a 0.76. Tenga en cuenta que comparamos el R-cuadrado ajustado porque toma en cuenta el número de valores y el tamaño de la muestra. Nuevamente, el coeficiente de intercepción no es significativo, por lo tanto, el modelo estimado puede representarse como: y = 0.67x₁+0.30x₂.

Tenga en cuenta también que podríamos haber referido a nuestros vectores de datos por sus nombres, por ejemplo

> LM (devuelve $ USA ~ devoluciones $ Canadá)
Llamar:
lm (fórmula = devoluciones $ USA ~ Devoluciones $ Canadá)
Coeficientes:
(Intercept) Devuelve $ Canadá
3.174E-05 9.275E-01

Gráficos

En esta sección demostraremos cómo usar R para la visualización de algunas propiedades en los datos. Ilustraremos cifras obtenidas por funciones como trama(), Boxplot (), Hist (), qqNorm ().

Gráfico de dispersión

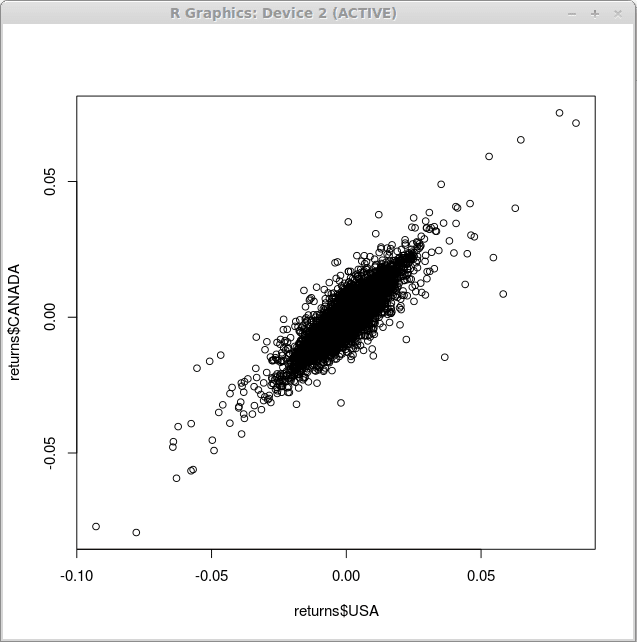
Probablemente el más simple de todos los gráficos que puede obtener con R es la trama de dispersión. Para ilustrar la relación entre la denominación del dólar estadounidense de los rendimientos del índice financiero y la denominación del dólar canadiense, utilizamos la función trama() como sigue:

> trama (devuelve $ EE. UU., Devuelve $ Canadá)

Como resultado de la ejecución de esta función, obtenemos un diagrama de dispersión que se exhibe a continuación

Uno de los argumentos más importantes que puede pasar a la función trama() es 'tipo'. Determina qué tipo de gráfico se debe dibujar. Los tipos posibles son:
• '"pag"'Por *p *oints
• '"l"'Para *l *ines
• '"b"' para ambos
• '"C"'Para las líneas parte solo de'" B "'
• '"O"'Para ambos'*o*verplotado '
• '"H"'Para'*h*istrogram 'como (o' alta densidad ') líneas verticales
• '"s"'Para la escalera *s *teps
• '"S"'Para otro tipo de *s *teps
• '"norte"'Para no trazar
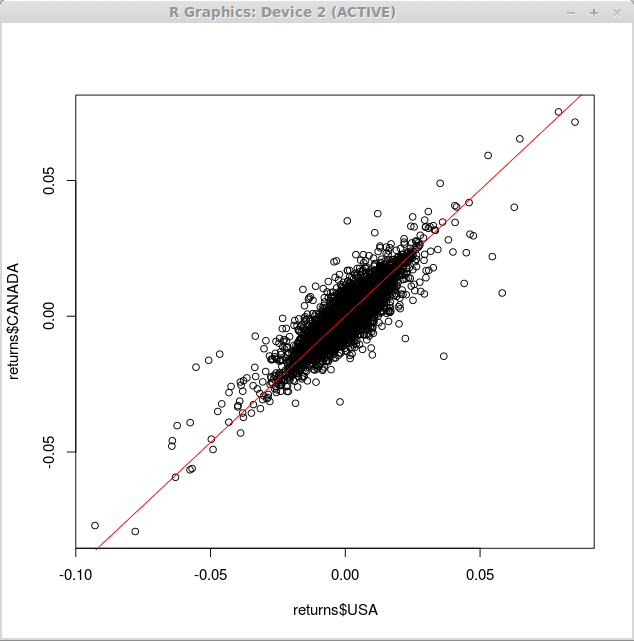
Para superponer una línea de regresión sobre el diagrama de dispersión arriba, usamos el curva() función con el argumento 'agregar' y 'col', que determina que la línea debe agregarse a la gráfica existente y al color de la línea trazada, respectivamente.

> curva (0.93*x, -0.1,0.1, add = verdadero, col = 2)

En consecuencia, obtenemos los siguientes cambios en nuestro gráfico:

Para obtener más información sobre la función plot () o líneas () use la función ayuda(), por ejemplo

> Ayuda (trama)

Trama de caja

Veamos ahora cómo usar el Boxplot () función para ilustrar las estadísticas descriptivas de datos. Primero, produzca un resumen de estadísticas descriptivas para nuestros datos por parte del resumen() función y luego ejecute el Boxplot () función para nuestros retornos:

> Resumen (devoluciones)
EE. UU. Canadá Alemania
Mínimo. : -0.0928805 min. : -0.0792810 min. : -0.0901134
1er QUS.: -0.0036463 1st quilla.: -0.0038282 1st quilla.: -0.0046976
Mediana: 0.0005977 Mediana: 0.0005318 Mediana: 0.0005021
Medio: 0.0003897 Media: 0.0003859 Media: 0.0003499
3 ° QuS.: 0.0046566 3rd quem.: 0.0047591 3rd quem.: 0.0056872
Máximo. : 0.0852364 Max. : 0.0752731 Max. : 0.0927688 

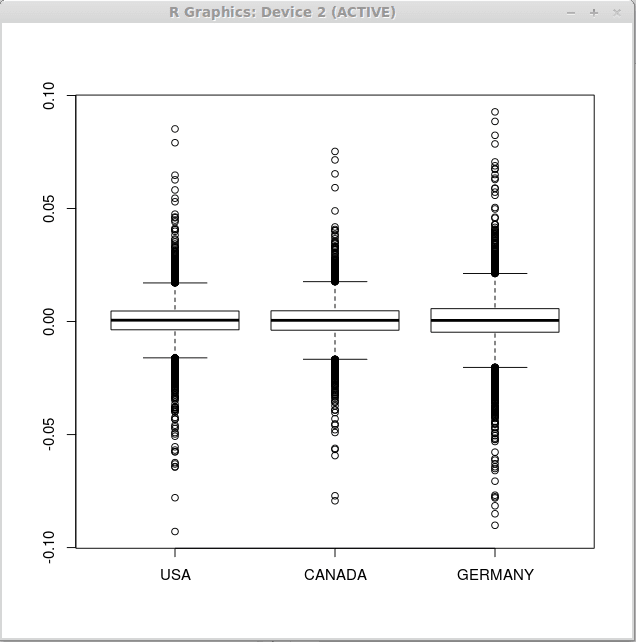
Tenga en cuenta que las estadísticas descriptivas son similares para los tres vectores, por lo tanto, podemos esperar diagramas de caja similares para todos los conjuntos de devoluciones financieras. Ahora, ejecute la función boxplot () de la siguiente manera

> Boxplot (devuelve)

Como resultado, obtenemos los siguientes tres diagramas de caja.

Histograma

En esta sección echaremos un vistazo a los histogramas. El histograma de frecuencia ya se introdujo en la introducción a GNU R en el sistema operativo Linux. Ahora produciremos el histograma de densidad para rendimientos normalizados y lo compararemos con la curva de densidad normal.

Permítanos, primero, normalizar los rendimientos del índice denominado en dólares estadounidenses para obtener media cero y una varianza igual a una para poder comparar los datos reales con la función de densidad normal estándar teórica.

> Retus.norma<-(returns$USA-mean(returns$USA))/sqrt(var(returns$USA))
> Media (Retus.norma)
[1] -1.053152E-17
> var (retus.norma)
[1] 1

Ahora, producimos el histograma de densidad para tales rendimientos normalizados y trazamos una curva de densidad normal estándar sobre dicho histograma. Esto se puede lograr mediante la siguiente expresión R

> Hist (Retus.norma, ruptura = 50, frecuente = falso)
> curva (dnorm (x),-10,10, add = true, col = 2)

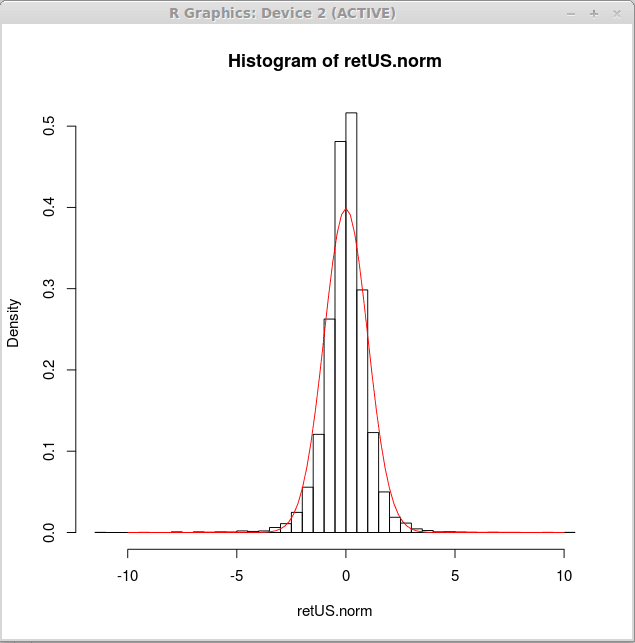
Visualmente, la curva normal no se ajusta bien a los datos. Una distribución diferente puede ser más adecuada para rendimientos financieros. Aprenderemos cómo ajustar una distribución a los datos en artículos posteriores. En este momento podemos concluir que la distribución más adecuada se recogerá más en el medio y tendrá colas más pesadas.

Plaza de QQ

Otro gráfico útil en el análisis estadístico es la trama QQ. La trama QQ es una gráfica cuantil cuantil, que compara los cuantiles de la densidad empírica con los cuantiles de la densidad teórica. Si estos coinciden bien, deberíamos ver una línea recta. Comparemos ahora la distribución de los residuos obtenidos por nuestro análisis de regresión anterior. Primero, obtendremos una trama QQ para la regresión lineal simple y luego para la regresión lineal múltiple. El tipo de trampa QQ que utilizaremos es la trama QQ normal, lo que significa que los cuantiles teóricos en el gráfico corresponden a cuantiles de la distribución normal.

La primera gráfica correspondiente a los residuos de regresión lineal simples se obtiene por la función QqNorm () de la siguiente manera:

> Devoluciones.lm<-lm(returns$US~returns$CANADA)
> QqNorm (devuelve.LM $ residuales)

El gráfico correspondiente se muestra a continuación:

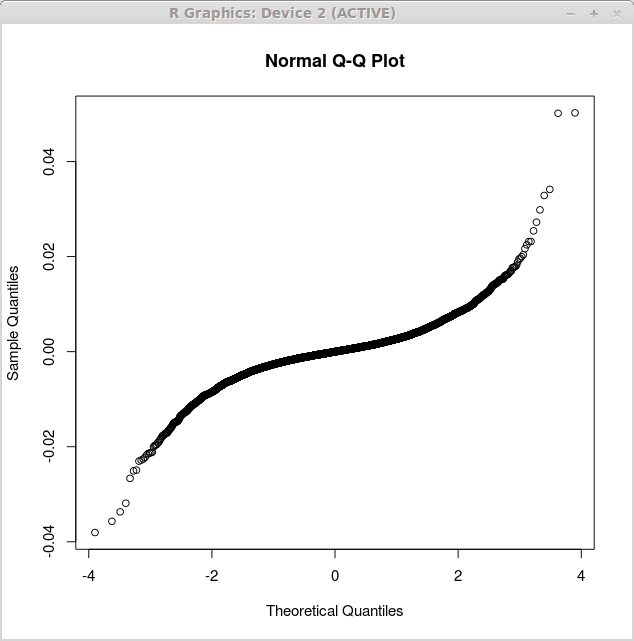
El segundo gráfico corresponde a los residuos de regresión lineal múltiple y se obtiene como:

> Devoluciones.lm<-lm(returns$US~returns$CANADA+returns$GERMANY)
> QqNorm (devuelve.LM $ residuales)

Esta trama se muestra a continuación:

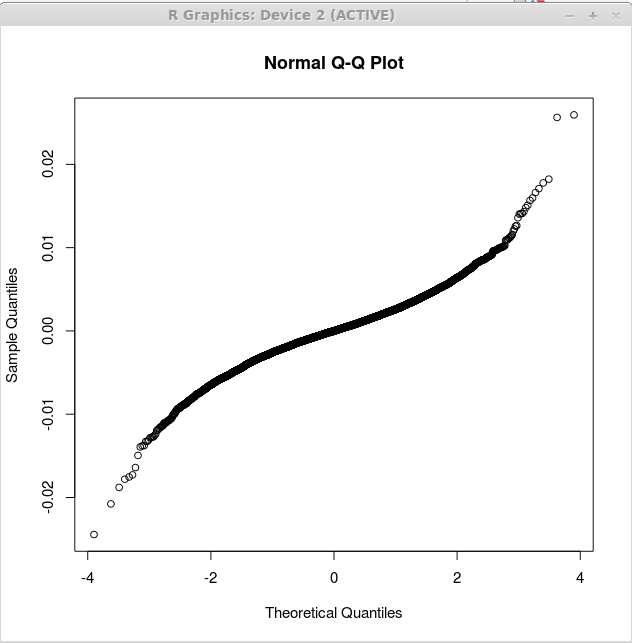
Tenga en cuenta que la segunda gráfica está más cerca de la línea recta. Esto sugiere que los residuos producidos por el análisis de regresión múltiple están más cerca de la distribución normalmente. Esto admite más el segundo modelo como más útil en el primer modelo de regresión.

Conclusión

En este artículo hemos introducido el modelado estadístico con gnu r en el ejemplo de regresión lineal. También hemos discutido algunos utilizados con frecuencia en gráficos de estadísticas. Espero que esto haya abierto una puerta al análisis estadístico con Gnu R para ti. En artículos posteriores, discutiremos aplicaciones más complejas de R para el modelado estadístico, así como la programación, así que sigan leyendo.

Serie de tutorial GNU R:

Parte I: Tutoriales introductorios de Gnu R:

1. Introducción a Gnu R en el sistema operativo Linux
2. Ejecutar Gnu R en el sistema operativo Linux
3. Un tutorial rápido de GNU para operaciones básicas, funciones y estructuras de datos
4. Un tutorial rápido de Gnu R a los modelos y gráficos estadísticos
5. Cómo instalar y usar paquetes en GNU R
6. Construyendo paquetes básicos en Gnu R

Parte II: Lenguaje GNU R:

1. Una descripción general del lenguaje de programación GNU R

Tutoriales de Linux relacionados:

• Una introducción a la automatización, herramientas y técnicas de Linux
• Cosas para instalar en Ubuntu 20.04
• Mastering Bash Script Loops
• Cosas que hacer después de instalar Ubuntu 20.04 fossa focal Linux
• Bucles anidados en guiones Bash
• Mint 20: Mejor que Ubuntu y Microsoft Windows?
• Manejo de la entrada del usuario en scripts bash
• Ubuntu 20.04 trucos y cosas que quizás no sepas
• Manipulación de Big Data para la diversión y las ganancias Parte 1
• Ubuntu 20.04 Guía