Conceptos básicos de matemáticas de la computadora binaria, decimal, hexadecimal, octal
- 1547
- 447
- Alejandro Duran
Cómo expresamos un número depende de si somos una computadora o un humano. Si somos humanos, es probable que expresemos números usando nuestro familiar 10-base sistema decimal. Si somos una computadora, es probable, en nuestro núcleo, de expresar números como De 2-base o binario.
Entonces, ¿qué pasa con todas las muchas formas de expresar números y por qué existe?? Este artículo entrará en detalles y, con suerte, al final contará Octal en sus dedos. Que funciona bien por cierto, siempre que use solo 8 dedos, después de todo ... Octal es 8-base.
En este tutorial aprenderás:
- Cómo hacer un conteo simple en sistemas no decimales como binario, hexadecimal y octal.
- Cuáles son los términos 2-base, 10 base, etc. apoyarlos y cómo entenderlos más fácilmente.
- La conexión entre estos diversos métodos para expresar números
Conceptos básicos de matemáticas de la computadora: binaria, decimal, hexadecimal, octal Requisitos y convenciones de software utilizados
| Categoría | Requisitos, convenciones o versión de software utilizada |
|---|---|
| Sistema | Independiente de la distribución de Linux |
| Software | Línea de comando bash, sistema basado en Linux |
| Otro | Cualquier utilidad que no esté incluida en el shell bash de forma predeterminada se puede instalar utilizando sudo apt-get instalación de utilidad de utilidad (o yum instalación para sistemas basados en redhat) |
| Convenciones | # - requiere que los comandos de Linux se ejecuten con privilegios raíz directamente como un usuario raíz o mediante el uso de sudo dominio$-Requiere que los comandos de Linux se ejecuten como un usuario regular no privilegiado |
Decimal
Todos estamos súper familiarizados con el sistema decimal: 1 a 10 o mejor 0 a 9, El mismo sistema nos pensó desde el primer día de clases e incluso antes por nuestros padres. Pero este sistema numérico no es todo. Es sólo uno de ellos. Llamamos a este sistema en particular 10-base ya que tiene una base de 10 caracteres, a saber 0 a 9.
En decimal, podemos contar fácilmente simplemente usando lo que nos pensaban: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
No necesitamos ejercer esfuerzo para esto, y es natural. Sin embargo, si realmente lo piensas, no hay una conexión lógica real entre la palabra número "cero" y "uno" y "uno" y "dos" y así sucesivamente. Seguimiento, con el tiempo entendemos que 0+1 = 1 y 1+1 = 2, Pero no hay directamente real y sustancial otro conexión entre uno y dos, 1 y 2. Es solo una forma de expresión.
Para ejemplificar esto, considere las afirmaciones anteriores en comparación con un ficticio 5-base sistema. Es mucho más difícil para nuestras mentes, ya que no han sido entrenados en el mismo, contar en un sistema de 5 base. Hagamos que sea un paso más duro y indicemos que nuestros 5 números se expresan como (, ), +, = y . respectivamente. Contamos hasta 11?
0: (1 :) 2: + 3: = 4: . 5 :) (6:)) 7:)+ 8:) = 9:). 10: +(11: +)
A la izquierda tenemos números decimales de 10 bases, a la derecha tenemos nuestro sistema numérico de 5 base autogenerado que cuenta de la misma manera (y tanto la izquierda como la derecha tienen valores numéricos iguales, I.mi. 10 en decimal/10-base es +( En nuestro sistema numérico de 5 base!).
Puedo contar muy fácilmente de esta manera, ya que estoy muy acostumbrado a cómo base X Los sistemas funcionan. Si mira un poco más de cerca el recuento, descubrirá rápidamente cómo funciona y verá cómo se compara bastante con nuestro sistema de conteo basado en decimales. La pista es esta; Una vez que te quedas sin personajes, simplemente prefijo el primer personaje con el primer personaje, haciendo dos personajes. Aún así, ¿cómo escribirías 100?? ¿Tienes que trabajar todo el camino por la lista?? Probablemente, ya que nuestras mentes no están acostumbradas a enumerar cosas usando estos símbolos.
Nuestras mentes entienden el decimal y luchan con la mayoría base X sistemas numéricos basados donde x no es 10. Quizás un ejemplo? Por favor calcule )) (((A ==-() b ... (+ donde hemos usado A para indicar la multiplicación y B es simple más. Pero no hay nada similar, ¿verdad?? Aún así, si convirtimos esto en decimales y nuestros familiares + y X símbolos, es probable que no encontremos estas ecuaciones difíciles.
Ahora que estamos armados con una comprensión de lo que base X Realmente es, el resto es mucho más fácil. Y lo prometo: no más símbolos extraños para expresar números, bueno, eso es hasta que llegamos a hexadecimal 😉
Binario
Hasta que las computadoras cuánticas lleguen a nuestras tiendas de computadoras locales, nuestras computadoras son bastante limitadas. Lo único, en su esencia, que una computadora entiende es fuerza o ninguna energía. Nada más! Una computadora simplemente entiende la alimentación o sin energía, pero no "entender" Que personaje a es, o que dígito 9 es. Todas estas cosas, y mucho más (yo.mi. todo el código de computadora) en su núcleo se expresa tanta potencia o ninguna potencia.
Una sola unidad de almacenamiento y expresión se llama poco. Un poco es la unidad de almacenamiento de más bajo nivel, núcleo de una computadora. A poco puede almacenar solo un solo 0 o un solo 1. En realidad, ni siquiera puede almacenar un cero o uno, solo puede almacenar energía (nuestra 1), o ningún poder (nuestro 0). Puede comenzar a ver cómo funciona 2-base, o binario, solo tiene dos expresiones: 0 y 1, Sin potencia o poder.
Si se imagina esto en términos de hardware de computadora física, puede imaginar una unidad de disco de tipo más antiguo como una placa llena de muchos lugares pequeños que tienen energía (están magnetizados) o no tienen potencia (no se magnetizan). Si lo imagina como datos que fluyen sobre un cable, puede imaginarlo como alimentación o ninguna alimentación.
Entonces, hagamos nuestro mismo contado a 11, pero esta vez utilizando nuestros dos únicos métodos de expresión posibles, los números en nuestro sistema numérico binario: 0 y 1.
0: 0 1: 1 2: 10 3: 11 4: 100 5: 101 6: 110 7: 111 8: 1000 9: 1001 10: 1010 11: 1011
A la izquierda tenemos decimal de 10 base, y a la derecha tenemos binario de 2 base.
Una vez tú Míralo, Es fácil de contar: simplemente comience con 0 y 1, y tenga en cuenta cómo 0 siempre tiene un significado especial: cuando llegas a 2 en decimal, no es 01 (i.mi. el primer personaje utilizado como un nuevo personaje más izquierdo), sino más bien 10 como 0 tiene el valor real de cero. En otras palabras, no escribiría: 0, 1, 2, 3, ..., 8, 9, 00 o 01, ya que ninguno tiene sentido; uno escribiría 10. Lo mismo se aplica aquí.
Lo mismo fue el caso en nuestro sistema de 5 base anterior: utilizamos ) ( para expresar el siguiente paso después de que se utilizaron todos nuestros dígitos, y no ( que sería incorrecto. Sería como escribir 00 en lugar de 6.
Una vez que conozca estos pasos básicos que se aplican a todos los sistemas X-base, se vuelve más fácil contar. Y puede usar seguir agregando un carácter más izquierdo y restablecer el carácter más a la derecha actualmente en uso, siempre que se quede sin posibles los siguientes pasos numéricos utilizando solo la longitud que tiene en este momento. Lea algunas veces de los pasos binarios y mire la progresión, y pronto podrá contar con binario, incluso sin usar dedos. Si usa los dedos, recuerde solo usar dos.
Hexadecimal
Entonces, ahora que hemos explorado 10 base, 2-base (y 5-base 😉 Veamos algo que puede parecer extraño nuevamente a primera vista: 16 base. ¿Cómo encajaríamos 16 posibles combinaciones numéricas en un solo carácter?? Bienvenido a Hexadecimal, que usa letras.
Hagamos un recuento simple primero: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
16 caracteres en total, el sistema hexadecimal usa A-F una vez que se queda sin formas de expresar el siguiente número en la serie. Contando de uno a 11 como lo hicimos anteriormente sería discutible aquí, ya que allí 11 es simplemente expresado por 'B'. Así que comencemos un poco más en el proceso esta vez:
0: 0 1: 1 ... 9: 9 10: A ... 15: F 16: 10 17: 11
A la izquierda tenemos decimal de 10 base, y a la derecha tenemos hexadecimal de 16 base. Por lo tanto, es más fácil recordar, tenga en cuenta que Hexa-Decimal nos hace pensar en 6-10.
Ay! Ahora terminamos con 10 en hexadecimal de 16 base realmente vale dieciséis en decimal de 10 bases! Esto puede ser ligeramente confuso y uno puede ver inmediatamente la necesidad de comprender claramente con qué sistema numérico estamos trabajando para evitar errores costosos.
Muchas calculadoras en varios sistemas operativos tienen un desarrollador o una configuración basada en computadora que se puede activar para funcionar con diferentes sistemas numéricos. Algunos van un paso más allá y le muestran muy claramente a qué se traduciría el número en cuestión en varios otros sistemas numéricos de base X, como esta gran calculadora incluida en Linux Mint 20:
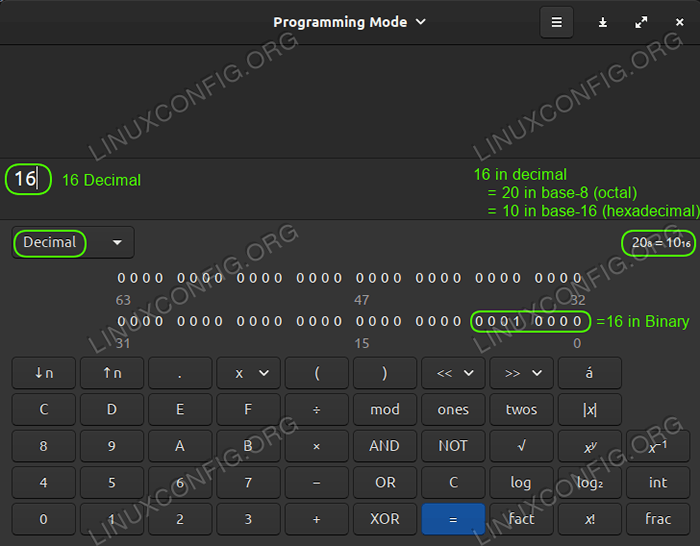Calculadora de Linux Mint 20 que muestra decimal, binario, hexadecimal, octal de una vez Octal
Ahora que hemos visto los sistemas numéricos anteriores, es más fácil ver cómo podemos contar en un sistema de 8 base, en este caso ser octal, Otro sistema utilizado junto con y por sistemas de procesamiento de computadora.
En octal, tenemos 8 caracteres numéricos que son 0, 1, 2, ..., 6, 7. Cuentemos hasta 11 en un sistema numérico de 8 base, comenzando a las 7:
7: 7 8: 10 9: 11 10: 12 11: 13
A la izquierda tenemos decimal de 10 base, y a la derecha tenemos octal de 8 base.
De nuevo podemos ver un ligeramente confuso 10 en el ser decimal de 10 base 12 en octal de 8 base.
Por qué tantos sistemas numéricos?
Entonces, ¿por qué hay tantos sistemas numéricos diferentes?? La razón es simple. Recuerda cómo una brote era una tienda para colocar un cero binario o otro? Bueno, si tomas 8 bits, tendrás un byte, y un byte a menudo se usa para expresar caracteres alfa-numéricos simples de un solo byte. Si piensa en cómo 8 realmente está en la base de esto, no debería estar demasiado lejos para ver que Octal (8) se ajuste a los sistemas numéricos que se utilizan en las computadoras.
A continuación tenemos hexadecimal, que es realmente 2 x 8 = 16 caracteres. Y aquí, tenemos 16 bits (o 2 bytes) representados como un solo personaje. Todo se cuelga de cerca, y realmente entra en juego cuando considera cómo se utilizan y procesan los personajes alfa-numéricos dentro de los sistemas informáticos. Por ejemplo, algunos caracteres especiales (como por ejemplo caracteres japoneses o chinos) pueden requerir dos o tres bytes para almacenarlos (multi-byte).
Varios sistemas numéricos simplifican los muchos tipos de flujos de datos que ocurren dentro de una computadora, y dependiendo de los flujos en cuestión, y cualquier algoritmo de computadora a juego seleccionado o utilizado, son posibles varias optimizaciones dependiendo del sistema numérico que emplee. La mayoría de los idiomas en desarrollo tienen, por ejemplo, un procesamiento binario altamente optimizado y potencialmente hexadecimal además del procesamiento decimal.
Conclusión
En este artículo, nos sumergimos en sistemas numéricos de 2 base, 10, 16-base y 8 base, siendo binario (2), decimal (10), hexadecimal (16) y octal (8). Vimos qué tipo de conexiones hay entre estas y cómo hacer un conteo simple en todos estos sistemas.
Aprender un poco más sobre cómo funcionan las computadoras a menudo ayuda, especialmente cuando se trata de hacer los primeros programas informáticos o comprender la teoría. Cuando uno se convierte en desarrollador a tiempo completo, en esa etapa, todos estos sistemas son de segunda naturaleza, y a menudo se usan dentro del código real.
Déjenos un comentario con sus ideas sobre estos sistemas numéricos! Y si está listo para aprender cosas más interesantes, eche un vistazo a nuestra manipulación de Big Data para la diversión y las ganancias del artículo de Parte 1! Disfrutar!
Tutoriales de Linux relacionados:
- Tutorial de depuración de GDB para principiantes
- Una introducción a la automatización, herramientas y técnicas de Linux
- Cosas para instalar en Ubuntu 20.04
- Mint 20: Mejor que Ubuntu y Microsoft Windows?
- Sistema colgado de Linux? Cómo escapar a la línea de comando y ..
- Cosas que hacer después de instalar Ubuntu 20.04 fossa focal Linux
- Cómo hacer cálculos decimales en BASH usando BC
- Mastering Bash Script Loops
- Ubuntu 20.04 Guía
- Cosas que hacer después de instalar Ubuntu 22.04 Jellyfish de Jammy ..